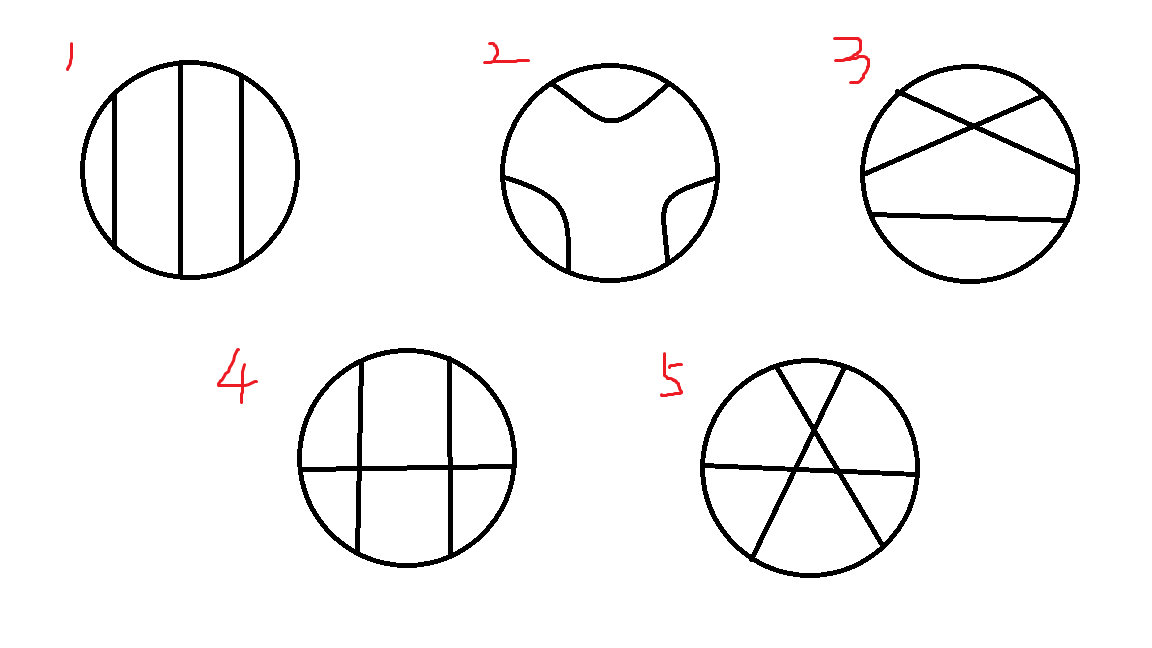Codeforces 297E - Mystic Carvings
好题。
因为只需要三条线段,直接分讨一下情况,实际上只有五种(CF 题解图片炸了,补一张自己画的)。

考虑所有限制,只有第二种和第五种是合法的,但是这两者都需要定一求二计算,很难算啊。
考虑正难则反,用总方案数 (3n) 减去第一、三、四种分别的方案数。
第一种很好算,断环为链以后就是二维数点,至于第三、四种分开算仍然难处理,需要合在一起算。
做完了。
在具体实现中,因为一根线把圆分成了左右两部分,我们只需要分别处理两边与其不相交的线段个数就可以了。
然后就是三、四两种情况会算重,取一半就行。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
|
#include <algorithm>
#include <iostream>
#include <cassert>
#include <cstring>
using namespace std;
using ll = long long;
using ull = unsigned long long;
using ld = long double;
class Fenwick{
private:
int tree[200005],n;
int lowbit(int x){
return x&(-x);
}
public:
int query(int x){
int ans=0;
while(x!=0){
ans += tree[x];
x -= lowbit(x);
}
return ans;
}
void update(int x,int k){
while(x<=n){
tree[x] += k;
x += lowbit(x);
}
}
void reset(){
memset(tree,0,sizeof(tree));
}
Fenwick(){}
Fenwick(int n):n(n){}
};
struct Element{
int a,b,l,r;
};
int n;
ull ans=0;
Element el[100005];
Fenwick fen;
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for(int i=1;i<=n;i++){
cin >> el[i].a >> el[i].b;
if(el[i].a>el[i].b){
swap(el[i].a,el[i].b);
}
}
fen = Fenwick(2*n);
stable_sort(el+1,el+n+1,[](Element x,Element y){
return x.a<y.a;
});
for(int i=n;i>=1;i--){
el[i].l = fen.query(el[i].b);
fen.update(el[i].b,1);
}
for(int i=1;i<=n;i++){
el[i].r += fen.query(el[i].a);
}
fen.reset();
for(int i=1;i<=n;i++){
el[i].r += fen.query(2*n)-fen.query(el[i].b);
fen.update(el[i].b,1);
}
fen.reset();
for(int i=1;i<=n;i++){
fen.update(el[i].a,1);
}
for(int i=1;i<=n;i++){
el[i].r += fen.query(2*n)-fen.query(el[i].b);
}
ull ans1=0;
for(int i=1;i<=n;i++){
ans1 += (ull)el[i].l*(ull)el[i].r;
}
ull ans2=0;
for(int i=1;i<=n;i++){
ans2 += (ull)(el[i].l+el[i].r)*(ull)(n-el[i].l-el[i].r-1);
}
cout << (ull)n*(ull)(n-1)*(ull)(n-2)/6-ans1-ans2/2 << "\n";
return 0;
}
|